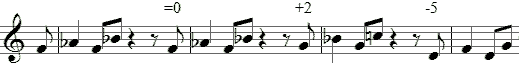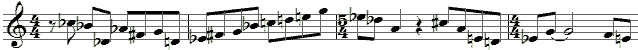Diminished fourth? A Greek secret

Posted on November 21, 2017 by jazzpanflute

I love listening to bouzouki players, especially when they improvise those rubato introductions to songs called taxim. They seem to be cramming semitones and augmented seconds wherever the fancy takes them.

It wasn’t till I started playing some Greek pieces myself, for a gig with a Bulgarian singer, that I realized there was some method in the madness.

Let’s look at the second half of a composition by Stavros Xarhakos called Horos tou Sakena. I’ve transcribed it the way it’s usually played, with all the grace notes.

Horos-tou-Sakena

Note that all the grace notes after the repeated notes are up a semitone, which is normal, as they serve merely for articulation, rather than acting as scale tones.

But when we look at the scale, we find a D minor with a lowered fourth, and two sevenths. In MOVES notation this gives (starting from D):

2 1 1 3 1 2 1  (total: 11)

or: D E F Gb A Bb C Db

Note that I haven’t completed the octave to the upper D, because the melody doesn’t do that either. Try continuing up to D and you see its spoils the effect of the scale – which to my ears is all about reaching for the unattainable.

The Greeks have a name for this scale, sampah pronounced sabakh, though they list it (on bouzoukispot.com) with a top D and no Db. Apparently, diminished fourths are allowed, but the line has to be drawn at diminished octaves!

Olivier Messiaen might have classed this as a defective form of his third mode of limited transposition (2 1 1 2 1 1 2 1 1) , on account of the missing G#, and would probably pencil in a top D to keep things tidy.

What do you think? You can listen to the whole tune in this bouzouki lesson video:

The part I have transcribed begins at 0:46.  Enjoy!

 

Posted in Uncategorized | Leave a comment

Serious noodling

Posted on March 15, 2016 by jazzpanflute

The whole point of having an intuitive instrument is to be able to follow the promptings of your Inner Ear without having to stop and think. Which scale is this? What note am I starting from? And much less: which notes are allowed?

You want to be able to start a run (or walk, whatever) without deciding in advance which scale you are embarking on. Just following your nose. Or rather ear. Your ear’s nose, if you prefer. Ace clarinettist Eddie Daniels calls this “noodling “.

Let’s assume that the noodle you are about to embark on will contain a mix of whole tones and semitones, some of them scalar and some passing, plus the occasional augmented second. You may feel like changing direction at any point. This is a known unknown, in Donald Rumsfeld’s immortal phrase. Stay with that.

The other known unknown, since you don’t even know what note you will be playing five notes from now, is what finger you will be using to play it with. Even pre-learnt scale fingerings have a habit of coming unstuck when a chromatic passing note shows up on a whim.

The common design element shared by intuitive instruments like the wholetone panpipes, the Pertchik vibraphone or the Lippens keyboard is the whole tone row. This allows the physical distance of the notes to faithfully reflect their intervallic distance. And this “isomorphism” is the basis of their claim to be intuitive instruments.

whole_tone_scale

All diatonic scales contain 3 notes from one whole tone row and 4 from the other. Semitones happen when you cross between the two rows; and the positions of these crossing points are what define the name of the scale you are playing.

Rather than learn 12 diatonic major scales and 72 modes, an intuitive instrument allows us to leap at will from one whole tone row to the other, without stopping to decide which scale we have defined.

But what about the physical interface? The presence of duplicate rows on the Jankó piano allows us the freedom to use the thumb at any point in any scale, avoiding the need to learn fixed patterns. But I said in my last post, freedom is not free. It comes at a price. If our noodling is to be serious – and exciting to listen to – we need to eliminate dither. Any hesitation about which stick or finger to bring in for the next note will break the flow.

The Lippens (Jankó) keyboard emancipates us from the need to think like pianists; but we will still need to develop both our melodic and our mechanical reflexes if we want to “play like singing in the shower”.

Which brings me to the exercises I have been working on for the Lippens keyboard, which are good for the Chromatone or any other Jankó-type keyboard. The idea is to be prepared for anything on the fly, any idea that comes to mind. For this we will use just five short scales:

(1 2), (2 2), (2 1 1), (1 3) and (3 2).

These five short scales are the building blocks of a vast range of noodling possibilities, including diminished scales, major, minor, blues, pentatonic and whatever takes your fancy. The first four make up so-called symmetrical scales if you stack them upon themselves.

For preparedness of the fingers, we will practice the five scales using two, three or four fingers in cyclical fashion.

1 2 , 1 2 3 , 1 2 3 4 , then 21, 231, 2341, 312, 3412, 4123

… and down again 4 3 2 1 , 3 2 1 , 2 1 …

The “shape” of the short scale will change depending on where the thumb comes in the cycle, as the thumb should be mostly limited to the bottom two rows.

Just to get you started, here is the (1 2) scale using two right hand cycles. There is no point in knowing which note is which, this being about intervallic awareness, so I won’t paint in the black notes:

lippen12scale

As you see, the shape changes at each turn of the cycle. The 1234 fingering cycle is simple and unchanging, so I will let you work it out for yourself! But to fully explore all the shape permutations with four fingers you will need to check out 2341, 3412 and 4123.

I believe the Lippens keyboard could soon be looking for crowdfunding to make it more widely available, so watch this space to be among the early adopters!

 

 

 

 

 

 

Posted in Intuitive Instruments, Scale Practice | Tagged , , , , , , , , , , , | 1 Comment

The Philosophy of Fingering

Posted on March 1, 2016 by jazzpanflute

Many moons have passed since I was last on speaking terms with film composers, so I was unable to ask John Williams if he was aware that his Imperial March for the latest Star Wars movie uses one of those Ethiopian scales I wrote about in a past post.

StarWars

Its semitone structure, if we take the tonic as G, is { 3 4 1 3 1 }. You would probably call this a defective harmonic minor. But if you start from the E-flat, you get { 3 1 3 4 1 } which looks a lot more like a major triad with approach (leading) notes. Considering the opening bar consists of an E-flat major triad, that’s a valid observation.

Some thirty years since I began designing logical piano keyboards and writing about them, I was recently privileged to receive a real one on loan, the majestically conceived Lippens keyboard. The Jankó equivalent of a concert grand in the way it feels, with great onboard sounds.

lippensPer

You can find demonstrations of this keyboard on youTube, including some lessons on fingering. You can visit their website and follow their Facebook page.

Since one of the reasons I gave up piano at an early age was being obliged to practice the 1231234 fingering for the major scale, I was alarmed to discover the same fingering being touted for the Lippens keyboard.

I had always imagined that the isomorphic design of the Jankó, as well as allowing me to use the same chord shapes in all transpositions,  would also allow me complete freedom of thumb undertuck because of the “redundant” extra rows. Specifically, the availability of those two front rows just for the thumb.

Looking at the design of the regular piano, you can see how using a 1231234 fingering avoids twisted thumbs and finger jams. But on a Jankó? Isn’t that what we wanted to get away from? The piano legacy? Scale practice?

Besides, as I mentioned in my post “What boys like“, which also applies to most jazzers I know, none of their favourite tunes actually use a naked major scale. Pink Panther. Simpsons. James Bond. Mission Impossible. Peter Gunn Theme. Hawaii Five-O. Any blues… and now the Star Wars Imperial March.

And what about those be-bop scales, that throw in a chromatic passing note in any one of 5 locations in the major scale. That’s an extra finger that has to come from somewhere!

Well it turns out, you can have freedom of thumb undertuck on one of these keyboards. But freedom is never free. You have to work for it. And the way I found is pretty simple really. It involves practising runs using three fingering cycles: 12, 123 and 1234, so that your thumb can find itself called upon at any degree of the scale. Its called preparedness!

Which brings me to…

The Philosophy of Fingering

Behind all the hours of scale practice lies the Big Unstated Assumption: that it will all someday be useful. It would be ridiculous for me to say that this ain’t so, but I would question it only in terms of ROI (that’s Return On Investment). Could our time be better spent? Not to mention what it does for our motivation.

As I said before, what our budding musician wants to do is play the damn tune! That’s his source of motivation. And each of those tunes he wants to play demands its own fingering solution. The advantage of the Lippens is that the fingering solution doesn’t depend on what key you’re in, and can be easily transposed to any other key once you’ve learnt it.

Playing the damn tune is also what I wanted to do on the Lippens keyboard. And the first tune I wanted to learn was Thelonious Monk’s egregious composition Trinkle Tinkle. While my boy wanted to learn that Star Wars March.

The other aim of scale practice, apart from memorizing the scales, is to train ten differently sized digits to hit those ivories with a constant force to create an even sound. Again, there is no reason this should be incompatible with freedom of thumb undertuck.

Cyclical fingerings can be practised two ways, depending on what we want to achieve. For evenness, we should use the 12 and 1234 cycles in triplet rhythm, and the 123 fingering in rhythmic groups of two or four.

For more accented playing, lay into the thumb (or fourth finger) and switch between the different cycles to put the accent where you want it. This is of course heresy to classical pianists, for whom accentuation should be independent of fingering choices.

But we all know that ain’t necessarily so.

 

 

 

 

 

 

 

Posted in Intuitive Instruments, Musicianship, Scale Practice | Tagged , , , , , , , , , , , , , | Leave a comment

The elephant in the music room

Posted on December 15, 2015 by jazzpanflute

This is a rant that I wrote some fifteen years ago, so some of the technological references are somewhat dated. But the rest still applies.

pianadap

Stop the ivories trade!

Many young people who begin piano studies or who just fool around on it never get beyond C major (or A minor) – the white notes.

Up to now, few music teachers have thought to lay the blame for this wastage of potential on the design of the keyboard, as if such a massive waste of effort and talent were par for the course.

How many educators have considered that a musical instrument, if it is to win adepts, must learn to compete with electronic games and other such expertly tested and targeted claims on the attention of the young?

The central concept in successful games design is the reward to difficulty ratio, a variable which should be carefully gauged at all levels.

Too easy and it becomes boring. Too hard and the player turns elsewhere.

In the case of the piano the solution has always been “carefully graded pieces”. But such fixed syllabi however attractively presented, ignore the main demand of the young: kids want to play their own stuff.

What’s so hard about the piano?

To answer this question let’s ask another. What’s so easy about a Nintendo games console? Why does Johnny spend all his pocket money in the arcade when he should be doing his practice?

And yet look at Johnny: in a short time he has developed amazing speed and reflexes on his instrument. Such a shame the only music that comes out are those pre-programmed chiptunes.

Now imagine we want to make him lose heart and go off his game. We could fix a bug in the game program so that when he hits the button that is supposed to deliver a swinging left hook to floor his opponent, his opponent hits him instead.

To avoid having Johnny adapt his strategy, we make it random. Just one time in a hundred to begin with.

But the rate doesn’t really matter. As soon as he’s aware of the problem, Johnny knows there is something wrong. He can’t fight on equal terms and he will lose points through no fault of his own.

This is serious: it means that there is no justice out there! So criterion number one for games designers: a consistent result for each action.

This has nothing to do with the piano, I hear you say. Each time I hit a B, I get a B. But I ask you, is that what you heard in your head, a B? If so, you are one of the lucky 3 percent who have perfect pitch. Go back to your piano and read no further. This is for the rest of you, the vast majority who have relative pitch and are in no sense less musically gifted – and can recognise a melody without knowing what key it’s in.

Lets give you a simple problem as an illustration. Go to the piano and starting from any note play the beginning of Yesterday. Just the melody.

Those of you who have only learnt the white notes (level one) will have a five in seven chance of getting it right.

Those of you who like to explore the other notes as well (level two) will find four different ways of getting the melody (which is your reward), namely white to white, black to black, white to black (jumping a white) and black to white (jumping a white).

But if you think any of these formulas will always get you Yesterday you are about to get annoyed. Their success rates, in the order given are: 5/7, 3/5, 2/7, and 2/5. You can only be 100% sure that moving to the left will get you a lower sound.

Level three is another cup of tea. By now we are acquainted with the degrees of the major scale and can guess that Yesterday begins on the second. So all we have to do is decide on a key, give it a name and count one tone up from it to start.

But wouldn’t it be nice to play music without that hassle? To play it the way we sing in the shower – without worrying what key we are in? And to have all the possibilities of the piano (and more – read on) on a genuinely gremlin-free keyboard?

The 6-6 keyboard

daskin_proto_v02

The Jankó keyboard is designed to meet the criterion 1 MOVE 1 interval, (thus rewarding the well placed finger with the expected sound) and has other advantages as well.

There are twelve times fewer chord shapes to learn, twelve times fewer scales to learn – if at all – and the stretch of the hand is reduced by 14% – without sacrificing roominess.

By permitting a single hand-form for each chord-type regardless of keynote, it provides the simplicity of the guitar.

Scale practice

One of the reasons the classical keyboard demands thousands of hours of mind-numbing scale practice is the problem of thumb undertuck. Prescribed fingerings for each scale have to be mastered in order to place the thumb in the correct place to avoid stumbles.

This can only be instilled by years of work.

The priority given to scales is the cause of a good deal of the friction between student and teacher and is one of the main reasons for the high dropout rate from piano lessons, not to mention lost childhoods.

The 6-6 keyboard offers complete freedom in the placement of the thumb undertuck. This is because every note can be played by either one of two or three keys arranged in rising receding rows so that the top key is easily reached by the fingers, while the lower one is convenient for the thumb.

This means that no matter what scale you are in, there are no bad habits to avoid! Which in turn means that you can practice exactly how and what you want and no “harm” can come of it. This releases teachers and students to explore less mechanical topics.

Like getting down to playing some music!

Posted in Intuitive Instruments, Music Education, Scale Practice | Tagged , , | Leave a comment

How do You Read Music?

Posted on November 6, 2015 by jazzpanflute

Well, how do you read music? Western music notation is unique in having adapted essentially one and the same system to the task of notating for all musical instruments and voices. But does that mean we all read the same way?

French musical education would have it so. Until recently, French kids had to endure a year of solfège before being allowed to handle the instrument of their choice – or of their teacher’s choice. Yes! If you were a year late starting violin they “demoted” you to viola.

The thinking behind the solfège system seems to be that you should be able to sing what you see on the page before attempting to play it on your horn. And that means singing the notename (do, re, mi…etc) – stripped of its alterations (sharp, flat) – with each note. You have to be fluent at this useless exercise to become a music teacher in France.

(Note that this is not the same method as tonic sol-fa, which notates the notes of a major scale from the tonic of whatever scale it happens to be.)

You might wonder how something designed as a code for instructing performers got perverted into a circus trick for sorting seven-year-olds into passed and failed.

I ask the question, because when playing a logical instrument like wholetone panpipes, bass guitar or Jankó keyboard you end up much more reliant on recognizing intervals on the page, rather than on your note-name reflexes. Since the same physical move always produces the same interval you only need to verify the starting note and away you go.

Saxophonists can rely on developing simple reflexes that send the fingers to a certain position at the sight of a certain note. It almost becomes like copy-typing. This can even extend to enharmonic distinctions:  an A-sharp on the page suggests going for a cross-fingering while a B-flat has him going for the side key or crunching the bis-key.

Trumpet players, and especially horn players, will definitely have to pre-hear what they see, at least approximately, just to get their lips, those invisible tone partners, tensing to the right frequency.

So which is it to be? Copy-typing, interval seeking or the-ear-is-king? Violinists continually switch between all three modes to achieve accuracy, especially in the upper positions. That is, until they stop having to think about it at all. In fact, that’s what they all say. There comes a point when you stop thinking about it.

At the master level, attained after the statutory 10,000 hours of playing from scores, it all becomes integrated. You read gestalts, hear what you see, and have the whole action in place before you go for the phrase.

So if it all boils down to a sort of Zen thing, it could be time we all learned something about meditating. That could be the missing ingredient for the dot-resistant millions out there!

Follow me on Twitter @jazzpanflute

Posted in Music Education, Musicianship | Tagged , , | Leave a comment

Chunking down on Scale Practice

Posted on November 2, 2015 by jazzpanflute

Why do we need full-length scales? Or: why do the scales we practise always need to span an octave? Why do we even need to think of them in that way?

Since all octave-length scales are composed of two chunks called tetrachords, why don’t we just practice those? Especially since most musical phrases fit inside one tetrachord (or pentachord). Taffanel had the idea in his Scale Game, reviewed in an earlier post.

Back in the day, your painting-box of available tetrachords in Western music contained:

2 2 1 major

2 1 2 Dorian aka minor

1 2 2 Phrygian

1 3 1 harmonic aka chromatic

and 2 2 2 Lydian.

This is of course just a small subset of possible interval stacks within the compass of half an octave. By adding the fifth (i.e. topping up the total to 7) we form pentachords. Your scale would then consist of a tetra- sitting atop a penta-chord.

My point is that, stacking any two of just these five elements (or the same one upon itself) creates a possible 25 scales, which when multiplied by the twelve houses means practising 300 instances of scales just to keep your ass covered, which to me seems excessive, and we haven’t even got to the blues yet!

Practising just these tetrachords (or pentachords) reduces the amount of elements you need to practise by a factor of 5! In addition, these elements are half the size.

Or put in broader terms: Just chunking down by a factor of two reduces the practice required by a factor of 2x where x is the number of possible chunks! And we can keep going, chunking on down!

Here is an excerpt from A Love Supreme part 1 where Trane is putting the 3 2 tetrachord through the houses:

lovesupreme

For the benefit of the curious, I list here the transpositions that follow (as always, in halfsteps): +6, -7, -1, +14, +1, -7, +5, -4, -4, +9, -6, +3, -7, +7, -10, +14, -5, +2, -5, -5, +2, +2, +1, +1, -3.

(There are prizes if you can see a pattern in that!)

Now my guess is, that 9 out of 10 jazz teachers will call this pattern “pentatonic”, i.e. part of a larger 5-note scale. So they might say, keep practising your pentatonic scales! They can say this on the basis of a figure that uses just three notes!

Moving on, Branford Marsalis wrote a very hip tune called Wolverine, which you should check out on the album Crazy People Music, and which contains this passage:

wolverine

containing an upward run tracing out these intervals: 1 3 1 3 2 2 2 3. We could of course arbitrarily select the octave from the D to the D and posit a scale (1 3 1 3 2 2), ignoring the fact that the remaining notes, E and G, invalidate the scale hypothesis by not stacking up the octave.

Or we could call the passage a hybrid between the well-known “augmented” scale (1 3) and the wholetone scale (2) straddled by the famed Trane lick a-birthed in Giant Steps 2 2 3.

I read somewhere (it could have been on jazzadvice.com – please add a search box widget guys!) that Michael Brecker’s secret to getting so much done was to only practice stuff he could actually use.

So why are we still whipping ourselves with octave-long scales?

My practice plan for learning a new instrument would begin by learning the smallest chunks in all twelve houses, and then recombining them or stacking them as the fancy takes me. I’m sure that this method would leave nothing uncovered, and would avoid the danger of installing annoying scale habits that we’re all tired of hearing (and of practising).

Not to mention the sweet, smooth learning curve.

In MOVES notation, all numbers in bold represent intervals counted in halfsteps or semitones. Rising and falling intervals are indicated by a + or a – sign. Numbers in parentheses () are interval arrays or scales that stack upon themselves. The term “houses” replaces the idea of keys or tonalities for cases where no identifiable tonal root is expressed.

Follow me on Twitter @jazzpanflute

Posted in Music Theory, Scale Practice | Tagged , , , , , , , , , , | Leave a comment

MOVES to the rescue !

Posted on October 31, 2015 by jazzpanflute

You would have thought that the bass guitar was one of the most logical and intuitive instruments around. It even beats the 6-string guitar because its tuning only uses fourths (=5 halfsteps), while the guitar slips in a stray major third (=4 halfsteps) between the G and B strings.

So you’d think you could almost learn it just by looking at it and thinking up jolly things to do. At the very least, the instrument promises to simplify life for the explorer impatient for musical adventure.

Now a friend has just shared this lesson for bass guitarists entitled Crackin’ the Slonimsky Code by one Joe Hubbard who claims to “demystify” two patterns from Nicolas Slonimsky’s famous Thesaurus of Scales and Melodic Patterns, which we have already reviewed in a previous post.

He has thoughtfully produced a pdf transcription of the patterns here. You can also find them in Slonimsky, numbered 394 and 496, in the grandly named “Sesquitone Progression” section, under the headings of Ultrapolation and Inter-Ultrapolation respectively.

In his presentation, Joe valiantly spells out the names of each note and explains the chromatic interpolations (to use Slonimsky’s term), and their application to altered dominant seventh chords.

And yet.

And yet I am left thinking, however useful such a breakdown might be for a pianist or a saxophonist, who are known to gobble up notenames like peanuts, why complicate things for the bass guitar? I can think of several great bass players whose brains would begin to disconnect with Joe’s presentation.

Joe admits: “It sounds more confusing than it is.” To which I answer: Why does it have to?

In science, progress is measured by the elegance of new theories. So why is music theory the royal exception? All the bass guitarist needs to know to learn the patterns presented in this lesson is encapsulated in this handy MOVES halfstep notation:

Pattern 1: {-1 +4}

Pattern 2: {-1 +2 +2}

Pattern 1 comes back down by the default method of reversing the signs:{+1 -4}. By the same token Pattern 2’s descending form is {+1 -2 -2} in Slonimsky, though Joe has composed his own version: {+1 +1 -2 -2 +1 -2}.

Now you don’t have to be a maths genius to notice that the linksums (sum of the numbers inside the wiggly brackets) are all ±3; and when you keep stacking 3‘s you get the diminished 7th chord. But even this fancy name is unnecessary knowledge, and might even trap some into thinking you need to chain the pattern four times for it to be somehow complete.

Notice also that both the ascending and descending forms of Pattern 2 use all 12 notes of the chromatic scale, which in MOVES we call the (1) short scale. But because Joe has set his mind on illustrating the octotonic diminished scales (2 1) and (1 2), he is obliged to dub the extra 4 notes “chromatic approaches” and “double chromatics”.

I don’t take issue with his pedagogy. It is conventional, and has doubtless helped a lot of players. But one little detail prompted me to write this post. Why choose that title? Crackin’ the Slonimsky Code? What did he crack? I feel underwhelmed.

And so I just thought I’d show you a small example of how MOVES notation really cracks code.  That’s crackin’!

Follow me on Twitter @jazzpanflute

Posted in Mappings, Moves notation, Music Theory | Tagged , , , , | Leave a comment

Get your first scale free?

Posted on October 9, 2015 by jazzpanflute

Remember all those collections they use to sell at the newsagents, offering you a free binder with the first instalment? As if you wouldn’t end up paying for it in the end! The idea was that once it was in your house you would have to find shelf space for it, and it would act as a weekly reminder to buy the next instalment and the next, and the next.

And if you didn’t follow through right to the end, you’d be left with an incomplete collection which would finish up unsold alongside all those electronic keyboards that turn up in garage sales. Not forgetting the piano tutor books that never got beyond the “free introductory” scale of C major – the white notes.

The design of the piano encapsulates the evolutionary stages of musical knowledge, so that the acquisition of pianistic skill mirrors in miniature the progression of Western music from Medieval organ music onwards. So you have to get the boring business out of the way before they let you learn the Super Mario Overworld Theme.

I noted in an earlier post entitled “What Boys Like” that their favourite tunes include themes from Mission Impossible, James Bond, the Simpsons and the Pink Panther, none of which use a standard major or minor scale. Many guitar students want to move straight onto blues scales.

So the free lunch is not only not free, but for some, may not even be that appetizing.

I have seen homemade panpipes made in different exotic scales, which end up on the mantelpiece once their possibilities have been exhausted. The Ecuadorian national panpipes called rondador has 17 tubes including (in this video at least) no less than three tubes sounding the upper E.

The tuning given by this informant is only one of several found in Ecuador and Bolivia. Since the tubes are meant to be played two at a time I give the resultant chords below.

rondador

This instrument is an extreme case of facilitating certain melodies at the expense of all the others. It embodies a set of fixed preferences, both melodic and harmonic.

Yet is this eccentric arrangement all that different from other Panflutes that offer the G major scale for starters, or even from the traditional piano? For me the difference is one of degree.

I mean, so long as we agree on having twelve equidistant intervals in an octave, why do we still give preference to one, boring, seven-note scale? Do the other five notes still need to be banished to the background?

The wholetone tuned panpipe is not intended to give preference to the whole tone scale. And in practice it doesn’t influence one to play more whole tone passages. It is simply the neatest and most logical way to pack the twelve notes of the octave, given that you can get two notes, a semitone apart, out of each tube.

Similar thinking led Paul von Jankó to design his keyboard back in the 1880’s. I was sent a video of a new model being played. Note that the title is “First Steps and Ideas on the Reinert Jankó Keyboard”. How different these first steps are from Chopsticks on the piano:

But I guess you need to experience how intuitive it is.

Posted in Intuitive Instruments, Mappings, Music Education | Tagged , , , , | Leave a comment

Inspiration

Posted on September 20, 2015 by jazzpanflute

Hammond organ wizard Cory Henry says he gets his inspiration from Jesus. Does that mean that atheists can’t get inspiration? No doubt, connection with some “higher” power helps a lot of people. But what if even that, for you, is malarkey?

Another question might be: does inspiration just boil down to having a good flow of ideas of what to play next? Without answering that, let’s watch MonoNeon dubbing his bass to the video you just saw:

So what drove him to overdub bass onto a track like that, apart from the inspiration he got from the track itself? This guy is motivated! To find out more, go to 4:35 and pause the video to check out MonoNeon’s art manifesto, just legible despite the low resolution:

Write your own vision and read it daily.

Have the southern soul/blues and funk at the bottom and the experimental/avant garde at the top… (YOUR SOUND!)

Make your life audible daily with the mistakes, the flaws… er’thang

Understand that some people are going to like what you do… and some are going to dislike it … when you understand and accept that dichotomy… move on!

Polychromatic color schemes. High visibility clothing

Childlike

Reject the worldly idea of becoming a great musician… JUST LIVE MUSIC

Here is another of my favourite musicians who does just that:

It might be worth making the distinction between inspiration – that uplifting of the spirit into a state of receptivity to some creative force – and sourcing, i.e. finding a rich vein of material to use in your playing.

Without inspiration, your playing might just become a meaningless stringing together of ideas that you have sourced from listening and practising.

Olivier Messiaen had plenty of sources, from birdsong to Indian tāla rhythms, but drew his inspiration from his religious faith. His synaesthesia – seeing colours in sounds – became part of his technique.

Here MonoNeon is sourcing his material from Cory Henry. And he has distilled his moments of inspiration into words of wisdom pasted on his wall to remind him of them and get him back into the Zone. It’s what keeps him aiming higher.

So where are you getting your inspiration from? What keeps you aiming higher? Even if you don’t believe in the supernatural, you have no shortage of inspirational quotes to pin on your wall.

But for me, the key advice from MonoNeon’s manifesto is the first sentence:

Write your own vision and read it daily.

Posted in Uncategorized | Tagged , , , , , | Leave a comment

Weightlessness

Posted on September 12, 2015 by jazzpanflute

Jazz education generally does its best to keep up with the latest trends in music, with thousands of teachers worldwide analysing classic performances and attempting to reverse-engineer them into exercises that you can try at home.

Working always on the assumption that you are playing over (or against) some cyclically recurring chord sequence, they offer examples of how certain geniuses allow themselves to fly in the face of conventional wisdom and play to some other arcanely related chord sequence that only they can hear in their heads.

The aim in certain styles seems to be to see how long you can spin it out for before succumbing to the need to touch base and play in key. The musical equivalent of the pioneering days of aviation: trying to stay aloft as long as possible without breaking one’s neck on landing.

And the thing that this is all striving towards, is the hardest thing to teach: a sort of musical weightlessness that needs no explanation to carry the listener with it. The weightlessness we experience in our dreams.

Or the weightlessness we suddenly feel when, after a calm exposition in C# minor of the haunting Brazilian folk tune Ogunde,  Trane suddenly wanders into another world, gently kicking the ground from underneath our feet with this:

weightless1

The first thing to note here, is that although highly chromatic, this is not “atonal” music. There are key centres, but they shift and float around each other. Just looking at the long notes that end some of the phrases provides a clue.

After revisiting the theme twice more, with some jagged passages in fourths in between, he brings us gently back to Earth:

weightless2

Looking at these passages, the jazz teacher’s reflex would be to ask: what kind of discipline leads to this level of artistry?  How to inculcate this?

Well, even if you learned the whole solo by heart and pulled out chunks of it in your own playing, you would never approach the process that gave birth to it.

So I want to ask: Wouldn’t it help us understand weightlessness if we asked what is holding us down? What comes between us and playing “like singing in the shower”?

In my quest for the perfect intuitive improvising instrument, which you can read about here, I noted the various “gravitational pulls” of the different instruments I have tried.

Folk instruments generally have a very strong pull. Players of the Japanese shakuhachi flute play the bottom note “ro” to anchor themselves, while many stringed instruments from Sitar to Erhu demand to be played in D or whatever.

And of course, a diatonic instrument like the button accordion, the Irish feadog, the Peruvian panpipes or the Chinese hulusi locks you into the home key after a few notes.

The instruments we play today are mostly descendents of folk instruments, having evolved from their village ancestors in the direction of greater weightlessness – or away from home-key dependence – without, however, emancipating themselves completely in every case.

Pick up any instrument, and start exploring ideas. Chances are, the instrument itself will suggest where to start.

Violin players looking for an idea will generally start in first position, often with the third finger. Trumpet players like to test their Bb and move on from there. You could say the instrument is trying to come between you and “playing like singing in the shower”.

You might think a saxophone would be free from this tendency. And yet even though there is no design constraint that pulls you towards it, force of habit often takes over. In my case I used to like to start from a note that uses all four fingers on one or both hands.

As a teenager, I wanted to improvise on the violin, but kept finding myself lured into the keys of D or G, perhaps by the lingering sound of the open strings I kept hitting accidentally. They actually keep ringing even when you don’t hit them. Unable to find a cure for this I moved on to other instruments.

Long story short, the only totally “weightless” instrument I have found in fifty years, has been the whole-tone tuned panpipes. I often find myself picking it up and going straight for the note I heard in my head, without knowing how that happened – as I don’t think I have perfect pitch.

On the liner notes to one of his Milestone albums, drummer Jack deJohnette relates how he took to practising the Melodica, a sort of keyboard-operated harmonica, in order to develop longer lines on the drums.

In like manner, being able to develop weightless lines on wholetone panpipes has allowed me to approach the violin again, and even to stay for long minutes aloft, despite the siren call of those pesky open strings.

So the best thing I can suggest, when you find yourself hitting those plateaux in your playing, is to find a cliff, and use a different instrument to jump off it.  And don’t forget to keep singing in the shower.

Posted in Intuitive Instruments, Musicianship | Tagged , , , , , , , | Leave a comment